Particle.news
Download on the App Store
5 ARTICLES
·
last wk.

New Mathematical Model Revolutionizes Bowling Strategy with Physics-Based Precision

Researchers unveil a six-equation system using Euler's formula to optimize bowling ball trajectories, offering a scientific alternative to traditional experience-based methods.

The new modeling relies on a ubiquitous equation known as Euler's formula.
A curved path is generally deemed the most effective way to score a strike
Jesus Quintana (John Turturro) licks a red bowling ball before throwing in a scene from The Big Lebowski
Image

Overview

  • A collaborative study involving MIT, Princeton, and other institutions has developed a mathematical model to optimize bowling ball placement and strike conditions.
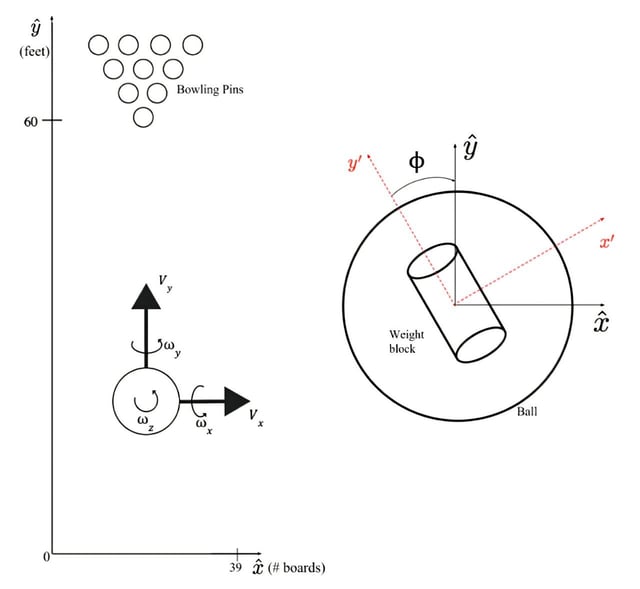
  • The model uses six differential equations derived from Euler's formula, treating the bowling ball as a rotating rigid body to calculate its trajectory.
  • Key variables such as lane oil distribution, ball asymmetries, and human error are integrated into the model, introducing a calculated 'miss-room' to improve accuracy.
  • The research aims to provide practical tools for players, coaches, and equipment designers, moving beyond subjective strategies to data-driven optimization.
  • Future enhancements to the model are planned, including adjustments for uneven bowling lanes, to further refine its application in competitive and training settings.